Recently, we had the exciting opportunity to showcase our approach at BETT 2025: Enhancing Open-Ended Math Questions with Instant Feedback to teachers, publishers and educators alike at the conference in London. Feedback plays a crucial role in guiding learning, and at the event, we focused on how instant feedback in open-ended math questions can dramatically enhance students’ mathematical understanding, all the while assisting teachers and making their day to day more efficient.
Unlike traditional multiple-choice problems, open-ended mathematics questions require deeper thinking as they are questions that a student can freely answer without a predefined format, making personalized feedback more vital. In this article, we will explore the significance of instant feedback in open-ended math questions and discuss how different types of feedback—corrective feedback, confirmatory feedback, and suggestive feedback—can help students improve.
Why Instant Feedback Matters in Open-Ended Math Questions
The Power of Feedback in the Learning Process
Feedback is integral to the learning process, helping students refine their thinking and improve their understanding. This is especially true for open-ended mathematics questions, where there is often no one right answer. In such cases, instant feedback in open-ended math questions can make a significant difference in guiding students toward the correct solution.
During BETT 2025, we discussed how instant feedback in math questions not only helps students correct mistakes quickly and builds their confidence but how it also assists teachers in the class environment making the teaching and learning process much more efficient.
Types of Feedback for Open-Ended Math Questions
Different types of feedback are required depending on the student’s needs and the nature of the question. The three main types of feedback we focused on at BETT 2025 are suggestive feedback, confirmatory feedback, and corrective feedback.
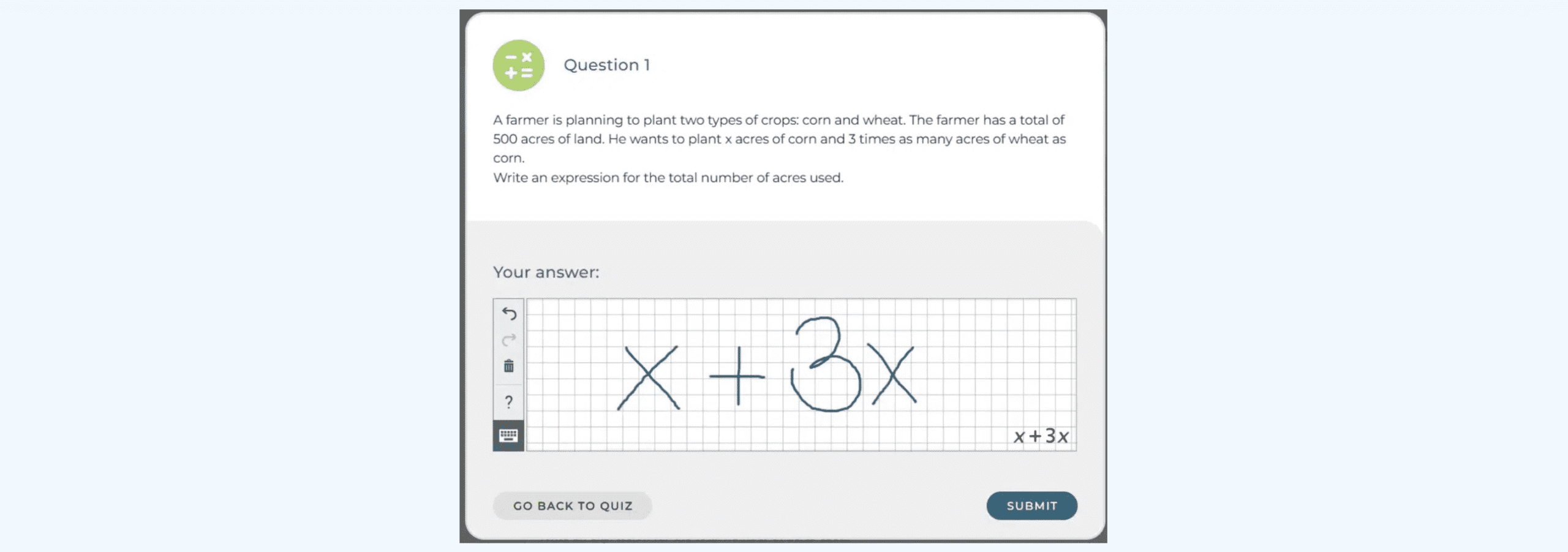
Suggestive Feedback in Math Questions
Suggestive feedback in math questions guides students to discover the solution themselves. Instead of providing the correct answer outright, suggestive feedback encourages independent problem-solving. For example, if a student suggests “2 and 8” as the two numbers whose sum is 10 and product is maximum, suggestive feedback might be: “What happens if you try numbers closer together?”
Confirmatory Feedback in Math Questions
Confirmatory feedback in math questions is designed to reinforce correct answers. When students solve problems correctly, feedback like “That’s correct, well done!” helps to affirm their understanding and boosts their confidence.
In the case of open-ended math questions, confirmatory feedback is invaluable for ensuring students stay motivated, especially when they are tackling complex problems.
This type of feedback fosters critical thinking and encourages exploration, making it an essential tool for developing problem-solving skills in open-ended math questions.
Corrective Feedback in Math Questions
Corrective feedback in math questions identifies mistakes and provides the correct answer. For example, if a student incorrectly solves x^2=4 as x=4, the corrective feedback would be “The correct solution is x= +-2”.
While effective for addressing misunderstandings, corrective feedback should be used in moderation, as over-reliance on it can hinder the development of problem-solving skills.
The Teaching Cycle: A Framework for Feedback Application
At BETT 2025, Mrs. Brook, a fictional high school math teacher, shared her teaching cycle, which integrates corrective, suggestive, and confirmatory feedback seamlessly. Her cycle is designed to maximize learning outcomes by aligning feedback strategies with the different stages of teaching.
The Four Stages of Mrs. Brook’s Teaching Cycle
-
Delivering the Content
Mrs. Brook begins her teaching by introducing and explaining the content to her students. This step ensures all students have a baseline understanding of the topic.
-
End-of-Class Knowledge Validation
Following the lesson, Mrs. Brook conducts an end-of-class knowledge check. This is where corrective feedback plays a crucial role. For example, if a student misunderstands a concept or calculation, Mrs. Brook provides immediate corrective feedback to clarify misconceptions.
-
Recommending Practice at Home
Mrs. Brook encourages her students to practice independently. At this stage, she often employs suggestive feedback to guide students without directly giving them answers, helping them to think critically and explore solutions. Additionally, confirmatory feedback is used to reinforce correct solutions and build student confidence. When students solve problems accurately, Mrs. Brook provides positive reinforcement such as “Great job!” to motivate them and affirm their understanding.
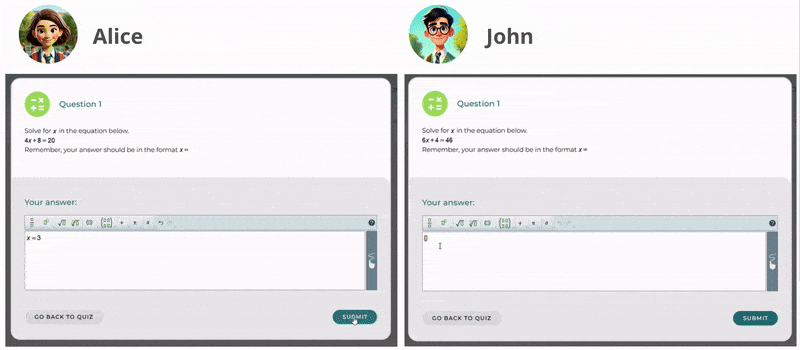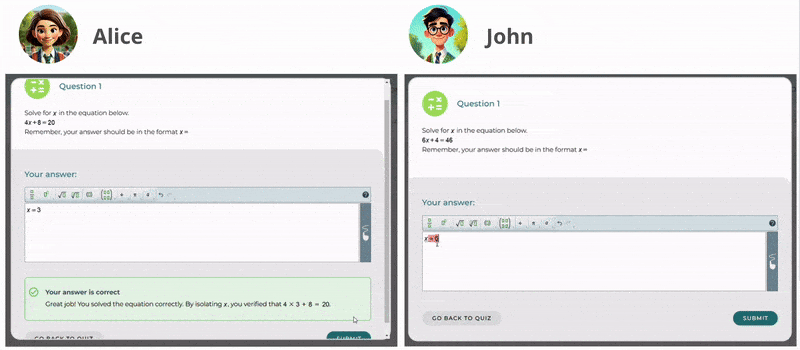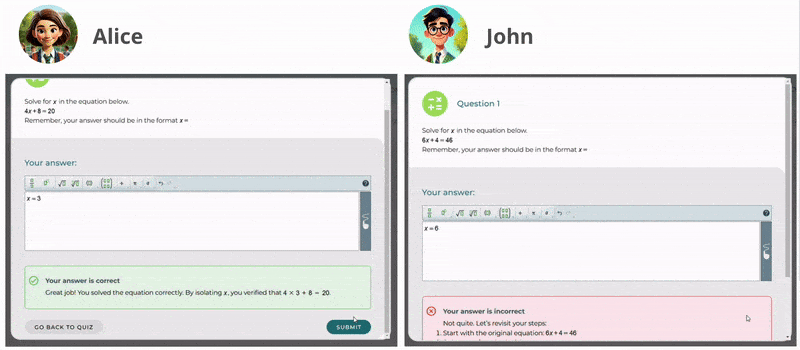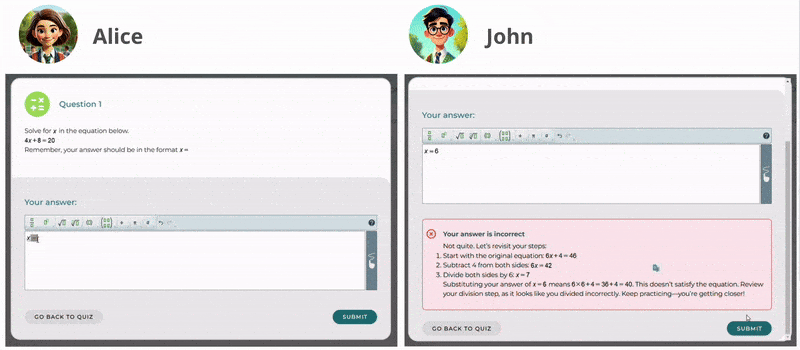
-
Assessing Students’ Knowledge Levels
After students have had the opportunity to practice, Mrs. Brook assesses their progress to identify areas of improvement. During this phase, she focuses on encouraging students to reflect on their learning journey and strive for continued growth. She fosters a positive environment by recognizing their efforts and offering motivation to help them stay engaged and confident in their abilities.
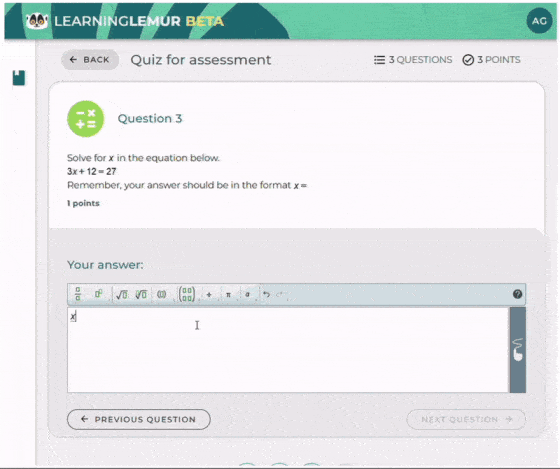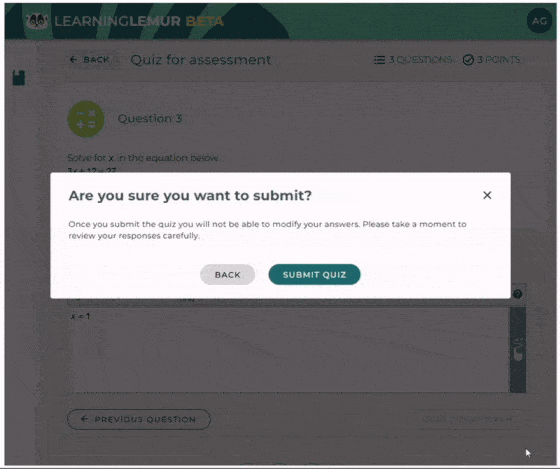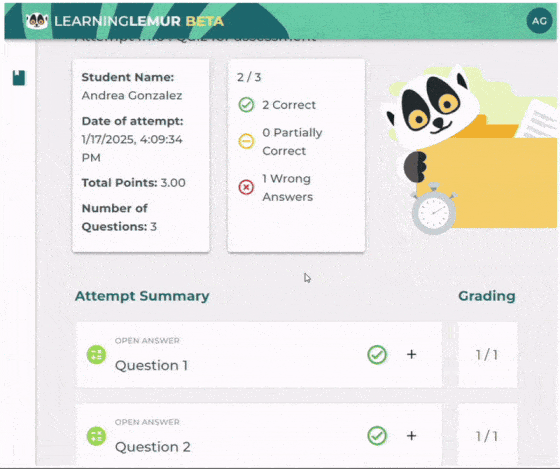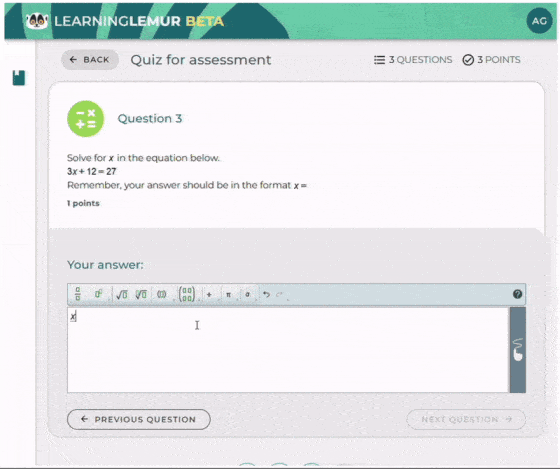
This cyclical model of teaching and feedback showcases how structured feedback enhances learning and ensures students’ needs are addressed at every stageTech.
Wrapping up: Embracing the Future of Math Education with Wiris
At WIRIS, we’re committed to supporting educators with the tools they need to provide effective feedback. Our Learning Lemur and WirisQuizzes products ensure that instant feedback in open-ended math questions is accessible and customizable, helping students succeed in their math learning journey.
As technology continues to evolve, the integration of instant feedback into open-ended math questions will only become more critical. We look forward to the continued evolution of math education, driven by personalized learning and real-time feedback.
