Learning mathematics requires more than just understanding theories: the key to mastering complex concepts and honing skills lies in continuous practice. However, traditional methods often limit the learning process: once the student has solved a problem, the challenge disappears, and exams often repeat the same questions, thus losing their value as an assessment tool. Imagine having the possibility to generate unlimited exercises with random variables, adapted to the needs of each student. With Wiris, this is now possible.
In addition, it has an automatic correction functionality which means that while the exercise is being generated, the answer is calculated simultaneously. This allows instant feedback, making it easier to learn and correct mistakes immediately.
For teachers, this tool offers a key advantage: the possibility of generating an infinite number of exercises, with each one being unique. In this way, teachers can create varied and personalized learning experiences, ensuring that students face new challenges every time they practice.
For their part, students enjoy constant practice which allows them to reinforce their skills without the worry of repeating the same exercises. In addition, this ability to generate unlimited exercises gives them excellent preparation for exams.
Practical example: Solving a system of linear equations
To illustrate how this tool works and how it can be used in the classroom, we will focus on solving systems of linear equations. We chose these types of problems because they represent a common mathematical challenge faced by all students and offer the possibility to explore different problem-solving methods. In addition, systems of equations can have various characteristics, such as being compatible, incompatible, or indeterminate, allowing students to work with a wide range of situations.
Let us imagine that we have the following system of linear equations with three unknowns: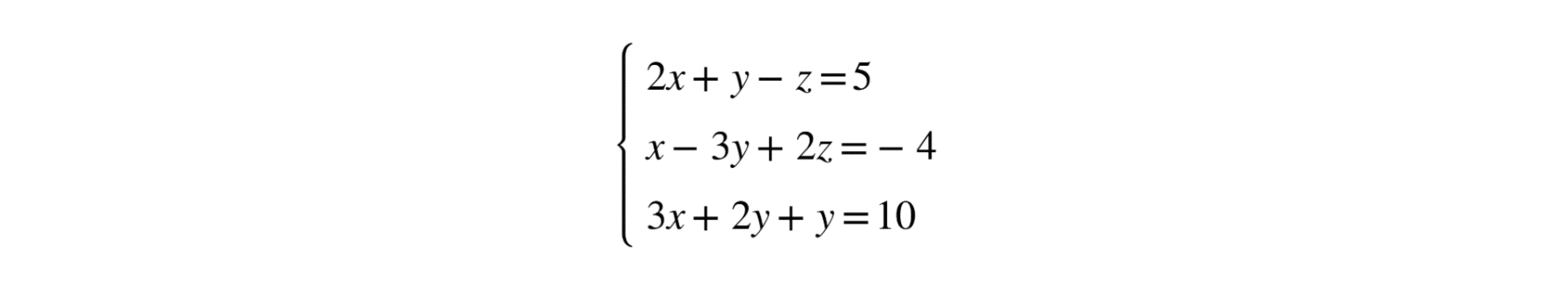
We are going to solve it using Gauss’s Method. The first step is to write the system in the form of an augmented matrix:
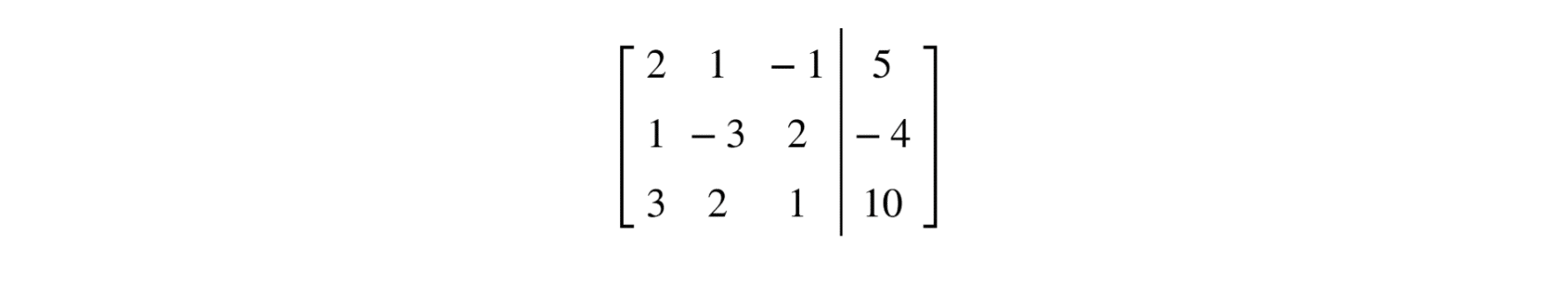
Now, we will apply elementary operations to reduce the matrix to its row echelon form.
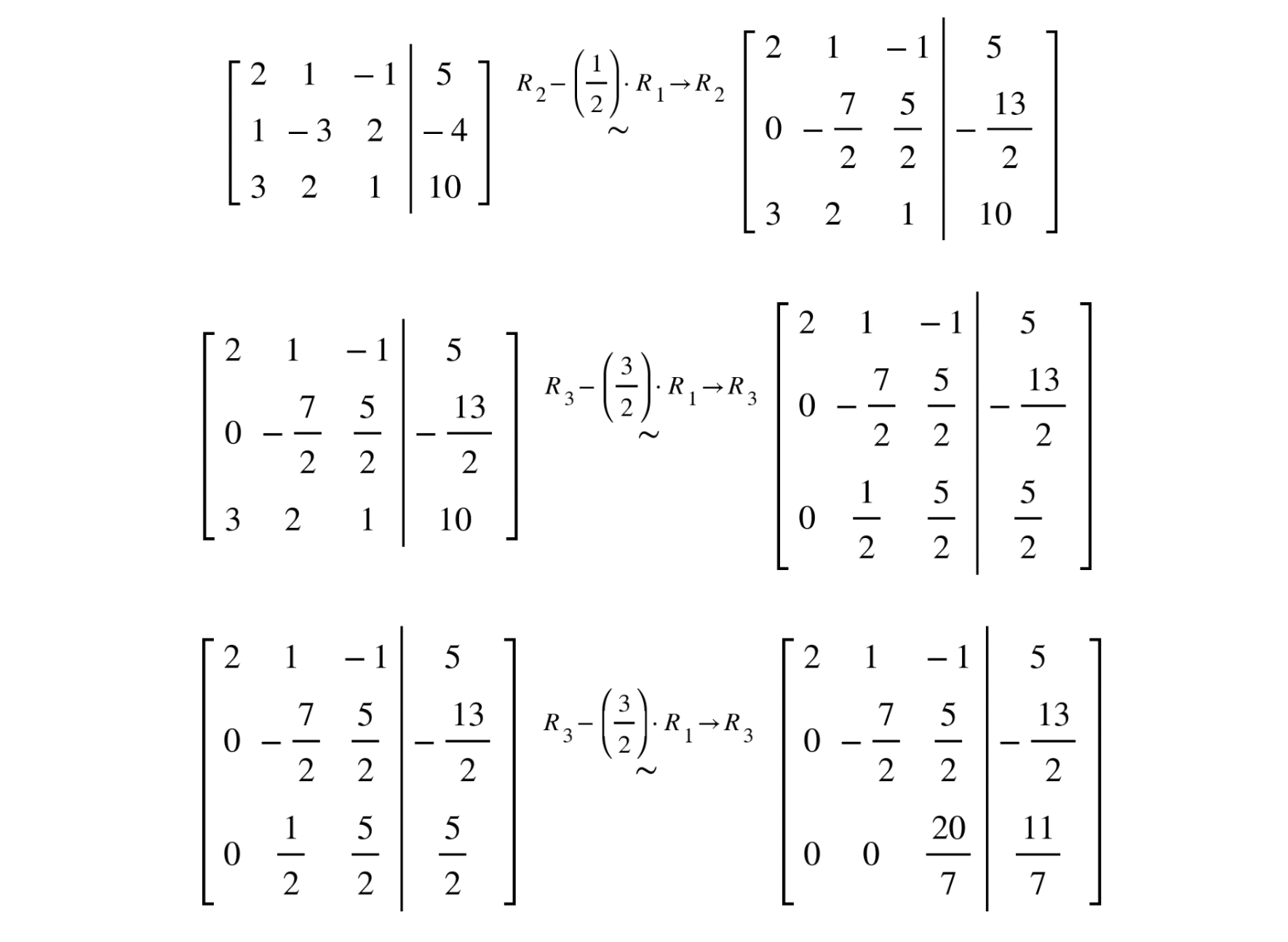
Therefore, we obtain:
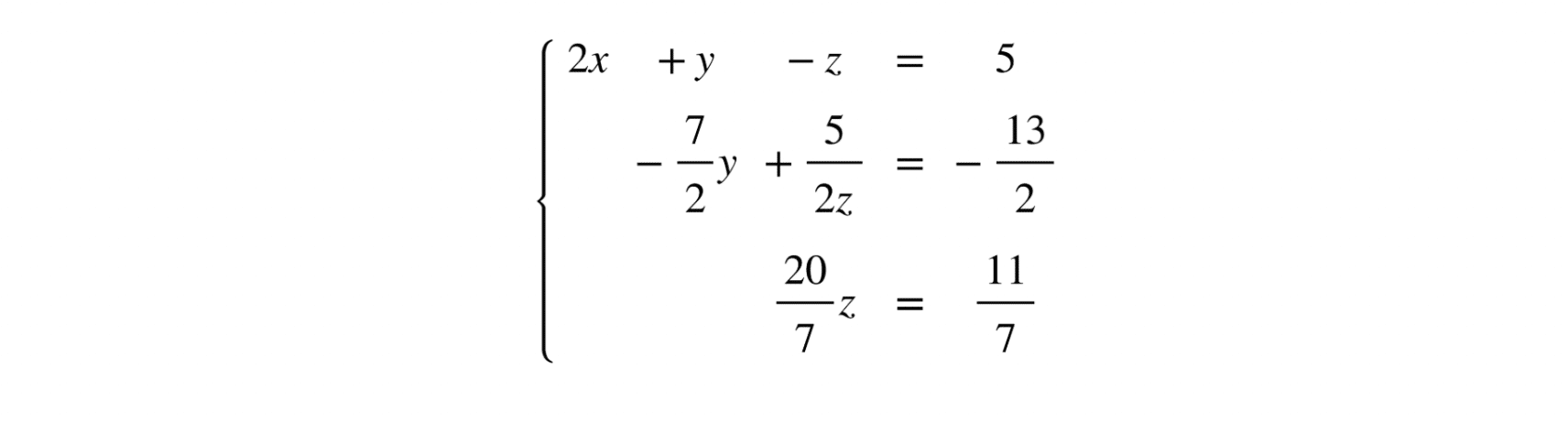
From equation 3 of the system, we find the variable z: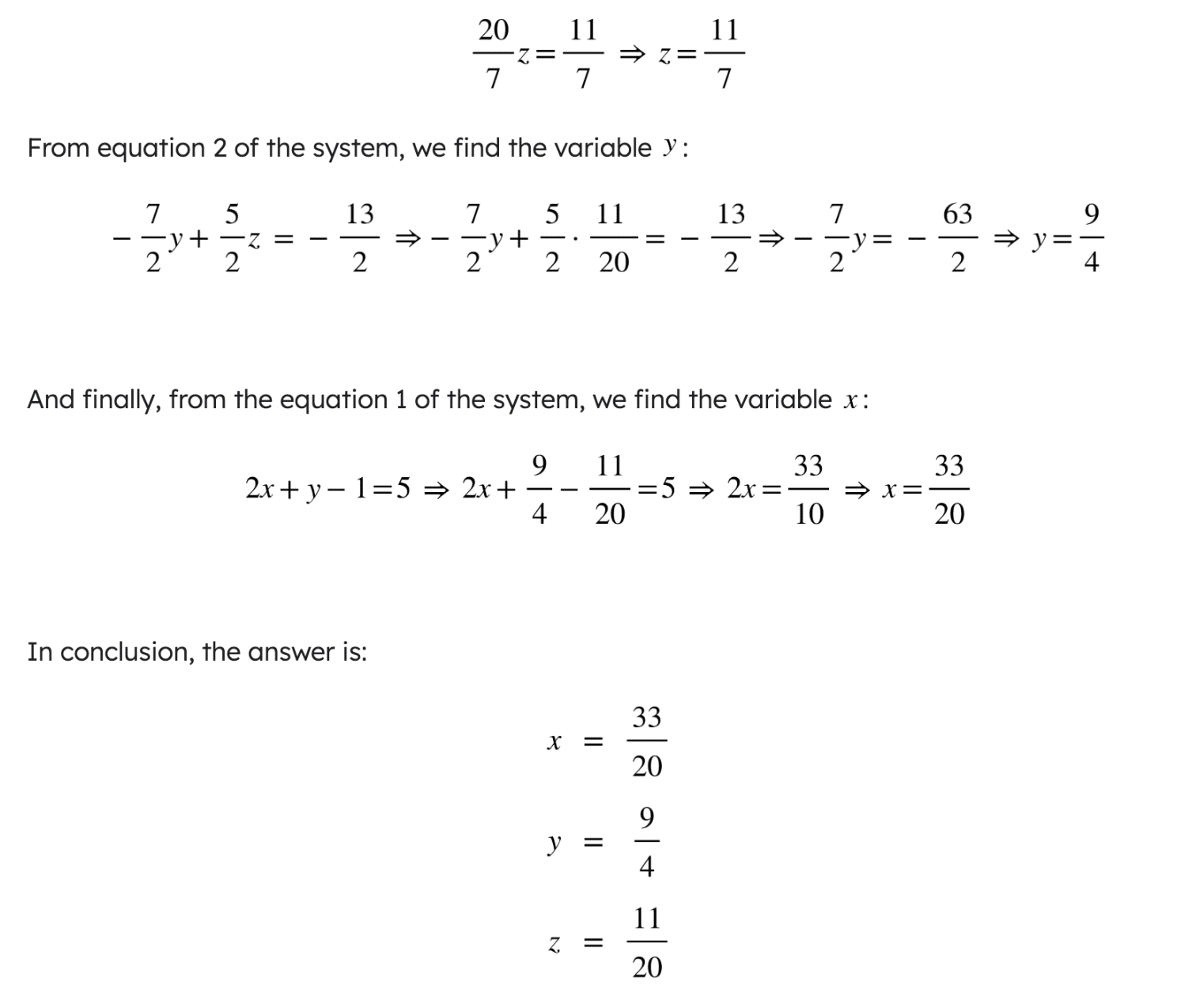
Unlimited generation of systems of linear equations with random variables
Now that we have solved this system, for further practice, we would like to be able to generate new systems of equations of the same form but with random values.
These systems would take the following form:
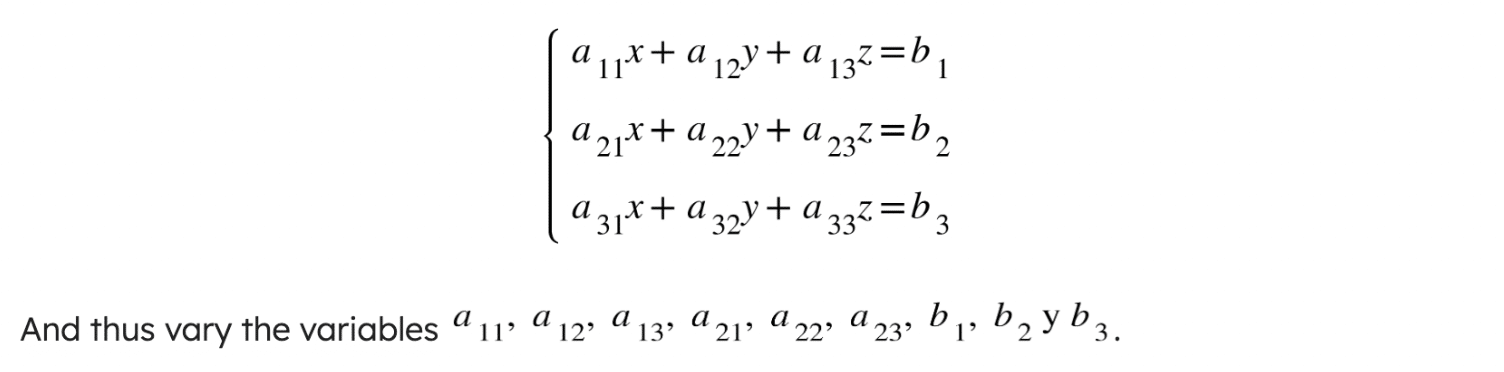
Below, we will show you a code example to implement this functionality and generate given random systems of equations. With Wiris, it is totally possible!
r() := random(-4,4)
sol = [r() with i in 1..3]
[a,b,c] = sol
repeat
A = [[r() with i in 1..3] with j in 1..3]
until determinant (A) != 0
b = A * sol
ec = {}
for i in 1..3 do
ecaux = A.i * [x,y,z]
ec = append(ec, ecaux = b.i)
end
{ec1, ec2, ec3} = ecr() := random(-4,4): This function generates a random number between -4 and 4.
sol = [r() with i in 1..3]: Here, three random values are generated that will represent the solutions of the system of equations.
[a,b,c] = sol: The generated values are assigned to the unknowns of the system.
repeat…until determinant(A) != 0: This block ensures that the coefficient matrix A is invertible (i.e., its determinant is not zero), which guarantees the system has a unique solution.
b = A * sol: The result vector b is calculated by multiplying the coefficient matrix A by the solutions sol
for i in 1..3 do: In this cycle, the three equations are generated, using each of the rows of the matrix A and the solutions sol.
{ec1, ec2, ec3} = ec: Finally, the three generated equations are stored in the variables ec1, ec2, and ec3, ready to be used in new exercises.
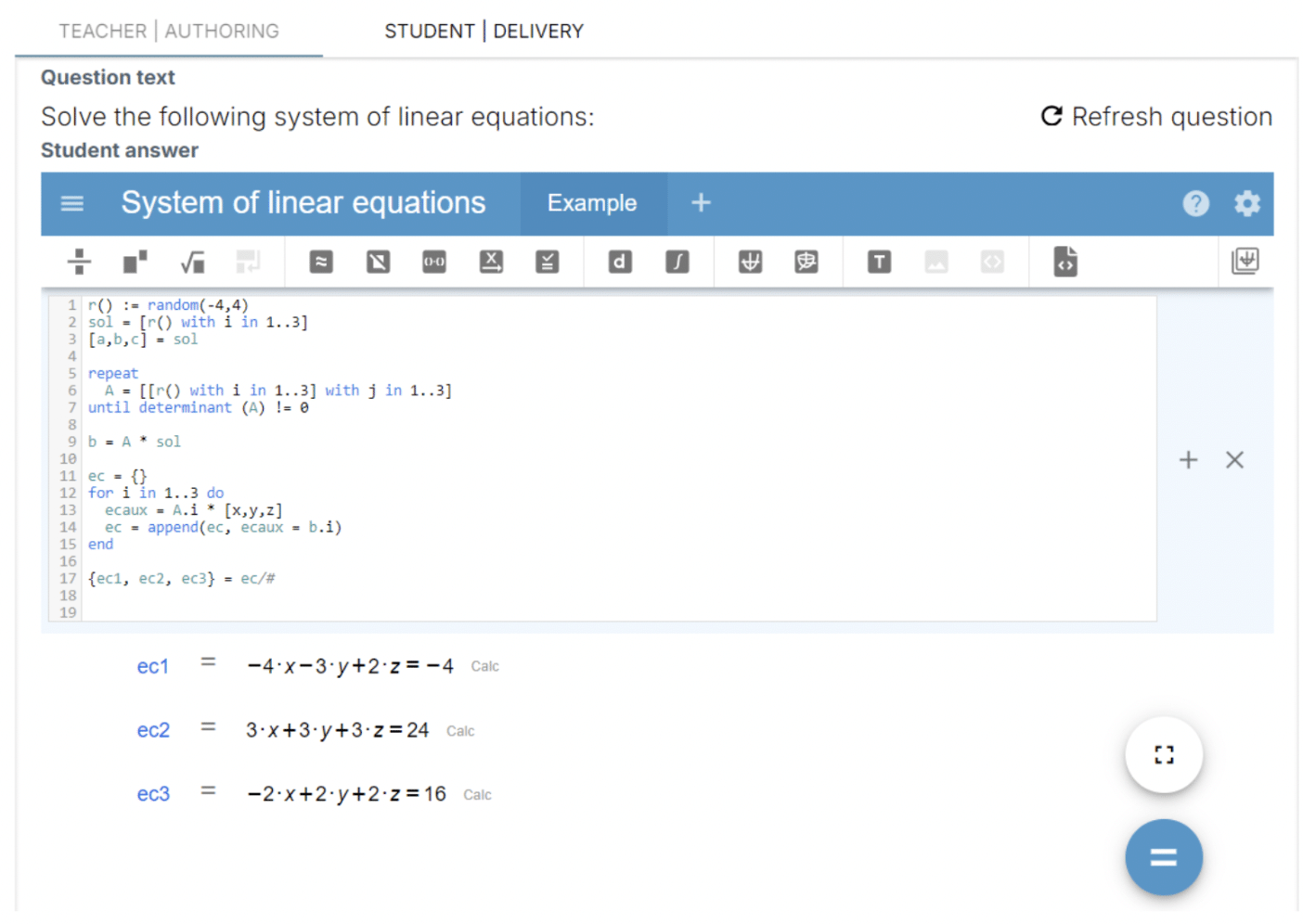
Using WirisQuizzes and implementing this code as a question, we can obtain the following results:
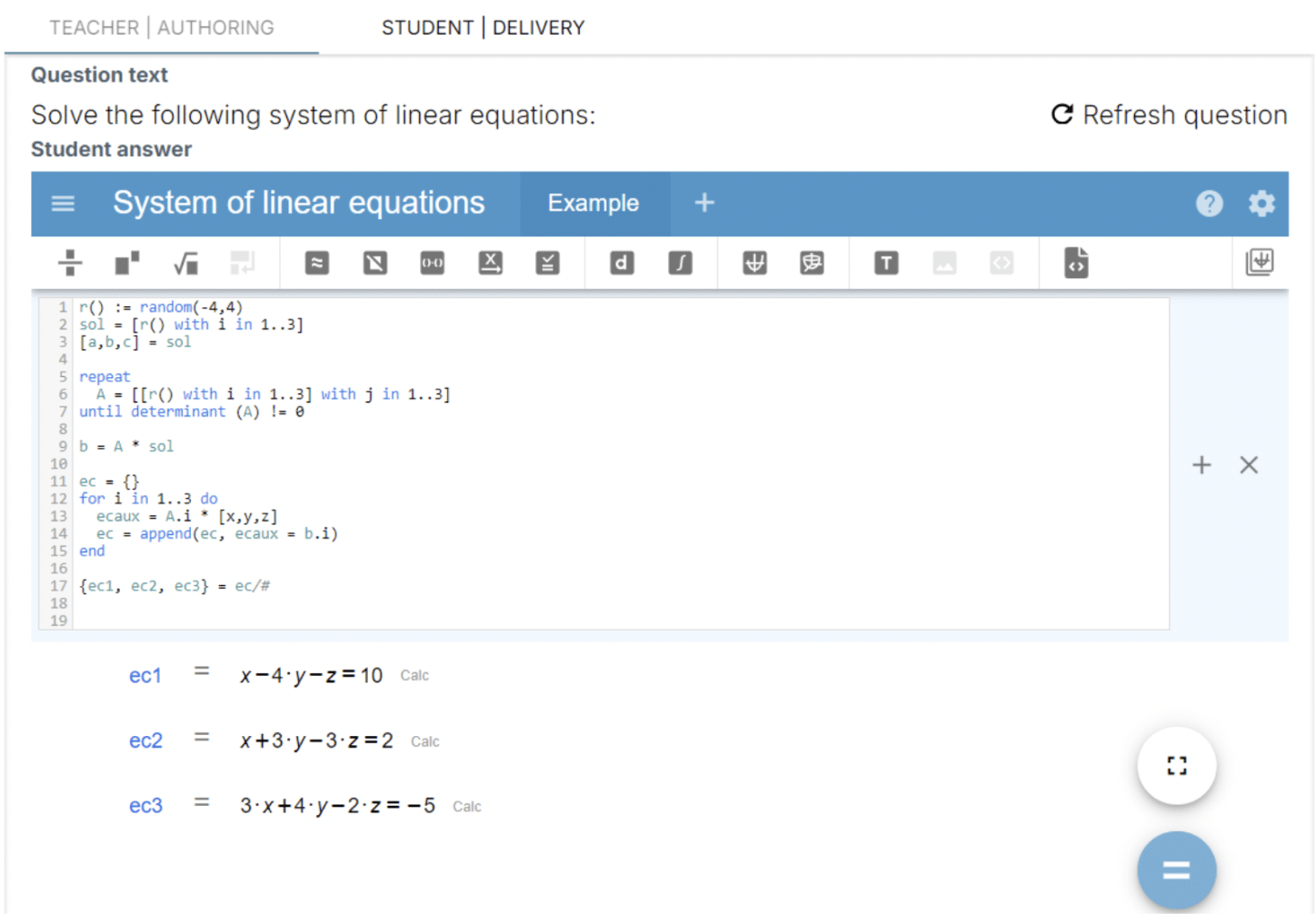
Reloading another system with the symbol “=” generates a new set of equations, as shown below:
For more details, you can consult the complete product documentation here.
If you have found this article useful, we would love you to share it with other colleagues, teachers or students. We would also be delighted to hear your opinion and any suggestions you may have.
Share









